Применение в здравоохранении. Средние величины – совокупная обобщающая характеристика количественных признаков



Средние величины – совокупная обобщающая характеристика количественных признаков. Применение средних величин:
1. Для характеристики организации работы лечебно-профилактических учреждений и оценки их деятельности:
а) в поликлинике: показатели нагрузки врачей, среднее число посещений, среднее число жителей на участке;
б) в стационаре: среднее число дней работы койки в году; средняя длительность пребывания в стационаре;
в) в центре гигиены, эпидемиологии и общественного здоровья: средняя площадь (или кубатура) на 1 человека, средние нормы питания (белки, жиры, углеводы, витамины, минеральные соли, калории), санитарные нормы и нормативы и т.д.;
2. Для характеристики физического развития (основных антропометрических признаков морфологических и функциональных);
3. Для определения медико-физиологических показателей организма в норме и патологии в клинических и экспериментальных исследованиях.
4. В специальных научных исследованиях.
Отличие средних величин от показателей:
1. Коэффициенты характеризуют альтернативный признак, встречающийся только у некоторой части статистического коллектива, который может иметь место или не иметь место.
Средние величины охватывают признаки, присущие всем членам коллектива, но в разной степени (вес, рост, дни лечения в больнице).
2. Коэффициенты применяются для измерения качественных признаков. Средние величины – для варьирующих количественных признаков.
Виды средних величин:
1) средняя арифметическая, ее характеристики – среднее квадратическое отклонение и средняя ошибка
2) мода и медиана. Мода (Мо) – соответствует величине признака, который чаще других встречается в данной совокупности. Медиана (Ме) – величина признака, занимающая срединное значение в данной совокупности. Она делит ряд на 2 равные части по числу наблюдений. Средняя арифметическая величина (М) – в отличие от моды и медианы опирается на все произведенные наблюдения, поэтому является важной характеристикой для всего распределения.
3) другие виды средних величин, которые применяются в специальных исследованиях: средняя квадратическая, кубическая, гармоническая, геометрическая, прогрессивная.
Средняя арифметическая характеризует средний уровень статистической совокупности.
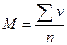
∑v – сумма вариант,
n – число наблюдений.
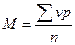
∑vр – сумма произведений каждой варианты на частоту ее встречаемости
n – число наблюдений.
Среднее квадратическое отклонение средней арифметической или сигма (σ) характеризует разнообразие признака
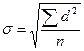
Σd 2 – сумма квадратов разности средней арифметической и каждой варианты (d = │M-V│)
n – число наблюдений
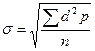
∑d 2 p – сумма произведений квадратов разности средней арифметической и каждой варианты на частоту ее встречаемости,
n – число наблюдений.
О степени разнообразия можно судить по величине коэффициента вариации 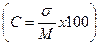
Если к средней арифметической величине прибавить и отнять от нее одну сигму (М ± 1σ), то при нормальном распределении в этих пределах будет находиться не менее 68,3% всех вариант (наблюдений), что считается нормой для изучаемого явления. Если к 2 ± 2σ, то в этих пределах будет находиться 95,5% всех наблюдений, а если к М ± 3σ, то в этих пределах будет находиться 99,7% всех наблюдений. Таким образом, среднее квадратическое отклонение является стандартным отклонением, позволяющим предвидеть вероятность появления такого значения изучаемого признака, которое находится в пределах заданных границ.
Средняя ошибка средней арифметической или ошибка репрезентативности. Для простого, взвешенного рядов и по правилу моментов:
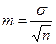
Для расчета средних величин необходимо: однородность материала, достаточное число наблюдений. Если число наблюдений меньше 30, в формулах расчета σ и m используют n-1.

При оценке полученного результата по размеру средней ошибки пользуются доверительным коэффициентом, которые дает возможность определить вероятность правильного ответа, то есть он указывает на то, что полученная величина ошибки выборки будет не больше действительной ошибки, допущенной вследствие сплошного наблюдения. Следовательно, с увеличением доверительной вероятности увеличивается ширина доверительного интервала, что, в свою очередь повышает доверительность суждения, опорность полученного результата.
Источник
Применение средних величин для оценки состояния здоровья населения
Средняя величина – количественная обобщающая характеристика однородной совокупности с изменяющимся варьирующим признаком. Виды средних величин и методы их вычисления. Оценка достоверности статистических показателей. Оценка физического развития населения.
| Рубрика | Медицина |
| Вид | курсовая работа |
| Язык | русский |
| Дата добавления | 10.11.2013 |
| Размер файла | 23,6 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Здоровье человека исследуется и измеряется на различных уровнях.
Понятие «общественное здоровье» по своей сути многогранно, не имеет общепризнанной формализованной структуры и пригодного для сопоставлений набора индикаторов. К показателям здоровья населения относятся показатели физического развития, заболеваемости, смертности.
Оценка физического развития имеет важное медико-социальное значение для многих областей медицины:
1) клинико-диагностическое (конституциональная диагностика);
2) изучение физического развития и его закономерностей в различных возрастно-половых группах населения;
3) динамическое наблюдение за физическим развитием и здоровьем в одних и тех же коллективах;
4) разработка региональных возрастно-половых стандартов для индивидуальной и групповой оценки физического развития детей;
5) оценка эффективности оздоровительных мероприятий (антропометрические показатели).
Данные о физическом развитии собирают в процессе специально организованных исследований. Полученные данные обрабатываются методом вариационной статистики, в результате чего получают средние величины роста, веса, окружности грудной клетки, используемые при индивидуальной и групповой оценке физического развития. Эти средние величины являются стандартами физического развития соответствующих групп населения.
Цель данной работы — рассмотреть средние величины и их применение для оценки состояния здоровья населения. Для этого решаются следующие задачи:
— дано понятие средних величин, рассмотрены их виды, свойства,
— изучен порядок вычисления средних величин,
— дана оценка достоверности статистических показателей,
— рассмотрено применение средних величин для оценки состояния здоровья населения на примере метода сигмальных отклонений и центильный метод).
1. Средние величины. Понятия. Виды. Свойства
Средняя величина — это количественная обобщающая характеристика однородной совокупности с изменяющимся варьирующим признаком.[5,c.39] Средняя величина — это число, выражающее общую меру исследуемого признака в совокупности. С помощью средних величин измеряют средний уровень изучаемого признака, то есть то общее, что характерно для него в данной совокупности.
Средние величины применяются:
1. для оценки состояния здоровья:
· параметров физического развития (средний рост, средняя масса тела, среднее значение жизненной емкости легких и др.),
· физиометрических показателей (средняя частота пульса, дыхания, АД, средний уровень сахара в крови);
2. для характеристики организации работы лечебно — профилактических учреждений:
· в поликлинике: показатели нагрузки врачей, посещаемость поликлиники, среднее число посещений на 1-м году жизни, среднее число детей на участке, среднее число посещений при определенном заболевании и т. д.,
· в стационаре: среднее число дней работы койки в году,
· средняя длительность лечения при определенных заболеваниях и т. д.,
· в санитарно-эпидемической станции: средняя площадь (или кубатура) на 1 человека, средние нормы питания в дневном рационе возрастных групп у детей и взрослых и т. д.;
3. для определения медико-физиологических показателей организма в норме и патологии в клинических и экспериментальных исследованиях;
4. в специальных демографических и социально-гигиенических исследованиях.
Существуют следующие виды средних величин:
· мода (Мо), она соответствует величине признака, который чаще других встречается в данной совокупности,
· медиана (Me) — величина признака, занимающая срединное значение в данной совокупности, она делит ряд на 2 равные части по числу наблюдений,
· средняя арифметическая (М), она в отличие от моды и медианы опирается на все произведенные наблюдения, поэтому является важной характеристикой для всего распределения.[5,c.41]
Другие виды средних величин, которые применяются в специальных или углубленных исследованиях:
Материалы антропометрических исследований подвергают вариационно-статистической обработке следующим образом:
а) путем составления вариационных рядов;
б) путем составления корреляционных решеток для основных признаков (рост и масса тела)
в) путем оценки основных антропометрических данных по таблицам центильного типа.
Основные свойства средней величины:
1) имеет абстрактный характер, так как является обобщающей величиной, в ней стираются случайные колебания;
2) занимает срединное положение в ряду (в строго симметричном ряду М=Мо-Ме);
3) сумма отклонений всех вариант от средней величины равна нулю.[5,c.42] Данное свойство средней величины используется для проверки правильности расчета средней. Она оценивается по уровню колеблемости вариационного ряда. Критериями такой оценки могут служить: амплитуда — разница между крайними вариантами, среднее квадратическое отклонение, показывающее, как отличаются варианты от рассчитанной средней величины; средняя ошибка средней арифметической (отношение среднего квадратического отклонения к квадратному корню из общего числа наблюдений — объектов).
Отличие средних величин от коэффициентов.
1. Коэффициенты характеризуют признак, встречающийся только у некоторой части статистического коллектива, так называемый альтернативный признак, который может иметь место или не иметь место (рождение, смерть, заболевание, инвалидность). Средние величины охватывают признаки, присущие всем членам коллектива, но в разной степени (вес, рост, дни лечения в больнице).
2. Коэффициенты применяются для измерения качественных признаков. Средние величины — для варьирующих количественных признаков.
2. Вычисление средних величин
Для вычисления средних величин необходимо построить вариационный ряд. Вариационный ряд — это числовые значения признака, представленные в ранговом порядке с соответствующими этим значениям частотами. Вариационные ряды бывают:
· простыми и взвешенными;
· сгруппированными и несгруппированными;
· открытыми и закрытыми;
· одномодальными и мультимодальными; с
· имметричными и несимметричными;
· дискретными и непрерывными;
· четными и нечетными.
Для определения Моды Мо необходимо выбрать величину признака (или варианта), которая чаще других встречается в данной совокупности.
Для определения Медианы Ме необходимо найти середину ряда. В ряду с четным числом наблюдений за Ме принимают среднюю величину из двух центральных вариант. При нечетном числе наблюдений Ме будет соответствовать центральная варианта, для этого (n-1)/2 ; где n- число наблюдений.
Средняя арифметическая М на равна среднему значению всех вариант в вариационном ряду:
средний величина статистический вычисление
где V — варианта, отдельное числовое выражение изучаемого признака;
n — общее число наблюдений.
Расчет взвешенной средней арифметической:
Получить Найти сумму произведений вариант на частоты,
где Vp— произведение каждой варианты на ее частоту,
n — общее число наблюдений.
Расчет среднеквадратического отклонения:
у = vУ d 2 р / n, (3)
где d — отклонение (разность) каждой варианты от среднеарифметической величины ряда (d = V — М),
р — частота («вес») варианты, число ее повторений в вариационном ряду,
Источник
Средние величины: определение, методика расчета. Оценка достоверности средних величин. Применение средних величин при оценке состояния здоровья (общественного и индивидуального).
Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.
Для вычисления средних величин необходимо построить вариационный ряд (ВР) –
1. ВР – это ряд чисел (вариант), характер-х изучаемый признак, расположенных в ранговом порядке (в убывающ или возрастающ последоват-ти) с соответствующими этим вариантам (V) частотами (Р).
2. V – варианта, каждое числовое знач-е изучаемого кол-венного признака.
3. Р – численность отдельной варианты в изуч совокуп-ти, величина, указывающ сколько раз встречается данная варианта в ВРу.
4. N – общ число наблюдений, из кот состоит ВР.
ВР применяется для определ-я средн ур-ня признака (средних величин) и ур-ней разнообразия признака (критериев разнообразия).
5. Построение вариационного ряда: а) Провести ранжирование вариант ряда, т.е. расположить их в убывающ или возрастающ последоват-ти б) Составить ВР вариант с соответствующими им частотами. в) Подсчитать число наблюдений (∑ p = n)
6. Виды ВР: 1) Прост– каждой варианте (V) соответствует частота р = 1. 2) Взвешенный – варианты в ряду встречаются с разн частотой (p > 1).
7. Преобразование ВР-в (группировка). — это способ укорочения ВР-а в целях ↓послед-х счетных операций.
8. Применение ср величин:
· Для оценки сост-я з-я: пок-ли физич развития, напр: ср вес, ср рост и т.д.; пок-ли соматич состояния, напр: ур-нь АД, ср ур-нь холестерина.
· Для оценки организации мед помощи: пок-ли деятельн-ти каждого врача в отдельности и лечебно-профилактич учреждения в целом, напр: ср число посещений в день к врачу, ср длительность лечения по отдельным заболев-ям. 3.В сан-противоэпидемич работе.
9. Свойства средней арифметической в вариационном ряду:
· Имеет абстрактный хар-р; Занимает серединное положение в ВР-у; Сумма отклонений всех вариант от средней равна нулю (на этом свойстве основан расчет М по способу «моментов»); Единство суммарного действия (S v p = M n).
10. Способы расчета средней арифметической (М). Среднеарифметический способ расчета применяется для вычисления среднеарифметической простой и среднеарифметической взвешенной.
М простая = S V М взвешенная = S V p
N n
ВРприменяется для определ-я ср ур-ня признака (ср величин) и ур-ней разнообразия признака (критериев разнообразия).
Оценка достоверности ср величин проводится по ошибке (m)
√¯n при большом числе наблюдений (30 и более);
для определения достоверности средней величины выборочной статистической совокупности при малом числе наблюдений (менее 30) используется формула:
Предельная ошибка показателя выборочной статистической совокупности ∆ равна 2 х m, то есть удвоенной ошибке. При этом вероятность безошибочного прогноза P равна 95%, то есть достаточна. Доверительный интервал получаем, вычитая из ср или относительной величины ∆ (предельной ошибки выборки) (получается нижняя граница интервала), а затем прибавляя к ней ∆ (получается верхняя граница интервала). В этом интервале с вероятностью безошибочного прогноза P , равной 95%, находится нужная нам средняя или относительная величина в генеральной совокупности.
Оценка достоверности различий ср величин по величине коэффициента t:
Если t = 1,96 и более, то различия достоверны.
Проведение диспансеризации определенных групп взрослого населения.
1. Диспансеризации подлежат следующие группы взрослого населения: — работающее население — неработающее население — обучающиеся в образовательных организациях.
Дис-я — комплекс мероприятий, вкл-й в себя проф мед осмотр и доп методы обслед-й, проводимых в целях оценки состояния з-я и осуществляемых в отношении определ групп населения в соответствии с законодательством РФ
Дис-я взрослого населения проводится путем углубленного обслед-я состояния з-я гр-н в целях:
1) раннего выявления хр неинфекц заболе-ий, являющихся осн причиной инвалидности и преждевр смертности населения РФ, ФР их развития, вкл-х ↑ур-нь АД, гиперхолестеринемию, ↑ур-нь глюкозы , курение, риск пагубного потребления алкоголя, нерац питание,↓ физ активность, избыт массу или ожирени, и потребления наркотич средств и и др ПАВ без назначения врача;
2) опред-я группы з-я, необходимых проф, лечебн, реабилитац и оздоровит мероприятий для гр-н с выявленными хр неинф заболев-ми и (или) ФР их развития, а также для здоровых гр-н;
3) проведения проф консультирования гр-н с выявленными хр неинф заболев-ми и ФР их развития;
4) определ-я группы диспансерного наблюдения гр-н с выявленными хр неинф заб-ниями и др заб-ниями, а также гр-н с ↑ и оч ↑ с-с риском.
Диспансеризация проводится 1 раз в 3 года за искл инвалидов Великой Отечественной войны и инвалидов боевых действий и тд, Годом прохождения диспансеризации считается календарный год, в котором гражданин достигает соответствующего возраста. Искл
маммография для жен от 51 до 69 лет и исслед-я кала на скрытую кровь для гр-н от 49 до 73 лет, кот проводятся 1 р в 2 года;
Основн особенностями нового порядка дис-и яв-ся:
— участковый принцип ее организации;
— возложение ответственности за организацию и проведение дис-и прикрепленного населения на руководителя ЛПУ и на отделение мед проф-ки, а ответственности за орг-цию и проведение дис-и населения терапевтич участка — на врача-терапевта участкового, врача общей практики.
— 2хэтапный принцип проведения дис-и;
— конкретизация понятия «факторы риска»;
-дифференцированный набор инструментально-лабораторных методов исследования;
— уменьшения числа групп з-я с 6 до 3х;
— обязат проведение проф консультирования в целях коррекции ФР уже в процессе дис-и.
Дис-я проводится при наличии инфор добровольн согласия гр-на или его закон представителя, данного по форме и в порядке, кот утверждены Минздрава РФ. Гр-н вправе отказаться от провед-я дис-и в целом либо от отдельных видов мед вмешательств
Врачом терапевтом участковым осущ-ся: составление списков гр-н, подлежащих дис-и в текущем календарн году, и плана проведения дис-и на текущ календарн год с учетом возрастной категории; мед осмотр гр-на по итогам 1 и 2 этапов дис-и, опред-е гр сост з-я, провед-е краткого проф консультирования, участие в оформлении учетно-отчетной документации и в оформлении паспорта з-я.
Кабинет мед проф-ки: инструктаж гр-н, прибывших на дис-ю, анкетирование, антропометрия, измерение АД, опред-е общ хл-на и глюкозы крови, измер-е ВД, формир-е комплекта документов, вкл-я заполнение уч формы «Маршрутная карта дис-и», учет гр-н, про шедших каждый этап дис-и, углубленное проф консультирование, заполнение паспортной части и, по согласованию с вр-терапевтом, др разделов паспорта з-я.
При подозрении или выявлении к-л забол-я, вр-терапевт направляет гр-на на доп обслед-е, не входящее в объем дис-и и осмотры специалистов.
Все гр-не по рез-там дис-и разделяются на 3 большие гр: 1.отн здоровые (I гр сост з-я), 2.лица с ↑ и оч ↑ суммарным риском развития ССЗ (II группа) и больные (III группа). Гр-не II гр сост з-я подлежат наиб активному проф вмешательству в рамках дис-и (углубленное и групповое проф консультирование)
БИЛЕТ 4
Дата добавления: 2019-02-22 ; просмотров: 307 ; Мы поможем в написании вашей работы!
Источник



