ABCD параллелограмм. АЕ биссектриса угла BAD, угол АЕС=132 градуса. Найти углы параллелограмма
Равенство углов САД и АДВ получим ин равенства треугольников АСД и АДВ, но давай попорядку.
АВСД — равнобокая трапеция, поскольку равны боковые стороны и диагонали.
Рассмотрим треугольники АСД и АДВ.
Стороны АВ = СД и ВД = АС по условию, сторона АД общая. Значит эти треугольники равны по 3 признаку. Из равенства этих треугольников следует равенство углов САД = АДВ.
Доказано.
Рассмотрим треугольники ВАС и СДВ.
Стороны АВ = СД и ВД = АС поусловию, а сторона ВС общая. Значит эти треугольники также равны по 3 признаку. Из равенства этих треугольников следует равенство углов ВАС = СДВ.
Доказано.
Верхний четырёхугольник рис.6,(слева буквы не видно,обозначим её Х):
ХО=МN (по условию),
OM=XN (по условию),
ОN=ON (общая сторона),
треуг.ОХN=треуг.ОМN по 3 признаку равенства треугольников (по 3-м сторонам).
Пусть х — коэффициент пропорциональности равный 1 гр. Тогда 0 0
Медиана равностороннего треугольника является его высотой и биссектрисой.
Медиана делит противоположную сторону пополам и разбивает треугольник на два равных прямоугольных треугольника с гипотенузой
16√3 и катетом 8√3
По теореме Пифагора
h²=(16√3)²-(8√3)²=256·3-64·3=576
h=24
Ответ. Высота= медиане = 24
Источник
ABCD-параллелограмм,AE-биссектриса угла BAD,периметр параллелограмма равен 56 см,BE:EC=3:1.Найдите стороны параллелограмма.
BC/4/5=AB/sin90 BC= 20
Пусть сторона АВ перпендикулярна к прямой 2x–y–1=0.
Это уравнение можно выразить с угловым коэффициентом:
y = 2x – 1.,Тогда угловой коэффициент к(АВ) = -1/2.
Уравнение АВ: у = (-1/2)х + в. Для определения в подставим координаты точки А: -3 = (-1/2)*5 + в, тогда в = -3 + (5/2) = -1/2.
Уравнение АВ: у = (-1/2)х — (1/2).
Сторона АС перпендикулярна к прямой 13x+4y–7=0.
Это уравнение можно выразить с угловым коэффициентом:
y = (-13/4)x + (7/4).Тогда угловой коэффициент к(АС) = 4/13.
Уравнение АС: у = (4/13)х + в. Для определения в подставим координаты точки А: -3 = (4/13)*5 + в, тогда в = -3 — (20/13) = -59/13.
Уравнение АС: у = (4/13)х — (59/13).
Точка С — это пересечение прямых АС и 2x–y–1=0. Приравняем:
(4/13)х — (59/13) = 2x – 1.
Координаты точки С: х = (-23/11), у = (-57/11).
Координаты точки пересечения высот
y=ax+b высот Точка D(пер_высот)
h(AC) -3,25 1,75 0,52381 0,04762
Координаты точки В находим как пересечение:
y=ax+b стор и выс Точка В
АВ -0,5 -0,5 0,81818 -0,90909
Координаты точки В: х = 0,81818, у = -0,90909.
Источник
На рисунке ABCD -параллелограмм, AE И DE — биссектрисы углов BAD И ADC соответственно, CD= 5 см. Найдите периметр параллелограмма и угол AED.
Биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам
Тогда AD=12х, а DC=8x
12x+8x=15
x=15/20=3/4
AD=12*3/4=9
DC=15-9=6
Треугольники АВС и ADP подобны по 3 углам
k=6/15=3/5
PD=12*3/5=36/5=7.2
Ответ:
Объяснение:
Угол РМВ смежный с углом НМВ
Угол РМВ=180°-угол НМВ=180°-136°=44°
Значит уг. СМВ=Угол РМВ :2=44°:2=22°
Угол МВС=углу НМВ=136°( как накрест лежащие)
угол МСВ=180°- уг. СМВ-угол МВС=180°-136°-22°=22°
трапеция АВСД.
АВ=10,5 дм
ВД=4 дм
Из угла В опусти перпендикуляр ВК на АД.
В прямоугольном треугольнике АВК угол А=60 град.
Значит угол АВК=90-60=30 град.
Против угла в 30 град. лежит сторона, равная 1/2 гипотенузы, а гипотенуза — это АВ=4 дм.
Значит АК=4/2=2 дм.
Основание АД=10,5. АВ=СД по условию, значит ВС=АД-2*2=10,5-4=6,5 дм
Источник
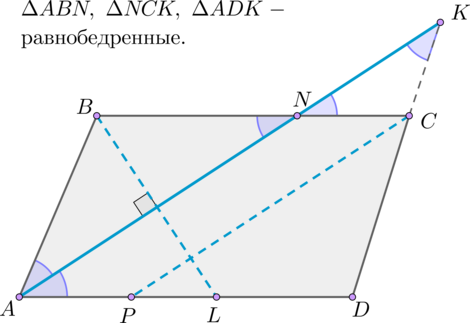
Параллелограмм: свойство его биссектрисы
Биссектриса параллелограмма — это отрезок, соединяющий вершину параллелограмма с точкой на одной из двух противоположных сторон и делящий угол при вершине пополам.
\(\bullet\) Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
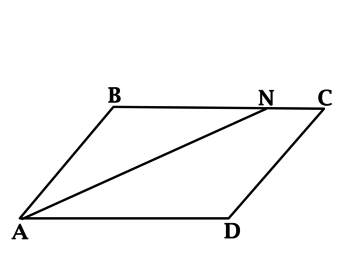
\(\bullet\) Биссектрисы соседних углов параллелограмма взаимно перпендикулярны: \(BL\perp AN\) .
\(\bullet\) Биссектрисы противоположных углов параллелограмма параллельны: \(AN\parallel CP\) .
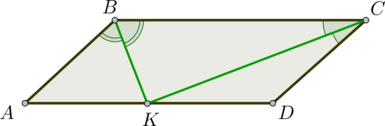
Биссектрисы углов \(B\) и \(C\) параллелограмма \(ABCD\) пересекаются на стороне \(AD\) . Найдите \(BC\) , если \(AB=4\) .
По свойству биссектрисы параллелограмма \(\triangle ABK\) и \(\triangle CDK\) – равнобедренные ( \(AB=AK\) , \(CD=DK\) ). Следовательно, \[BC=AD=AK+DK=AB+CD=2AB=8.\]
В параллелограмме \(ABCD\) проведены биссектрисы \(AN\) и \(BM\) , \(\angle ABM = 58^<\circ>\) . Найдите \(\angle BAN\) . Ответ дайте в градусах.
Сумма односторонних углов при параллельных прямых и секущей равна \(180^<\circ>\) , тогда \(\angle DAB + \angle ABC = 180^<\circ>\) .
Так как \(AN\) и \(BM\) – биссектрисы, то \(\angle BAN + \angle ABM = 0,5(\angle DAB + \angle ABC) = 90^<\circ>\) .
\(\angle ABM = 58^<\circ>\) , тогда \(\angle BAN = 90^ <\circ>— 58^ <\circ>= 32^<\circ>\) .
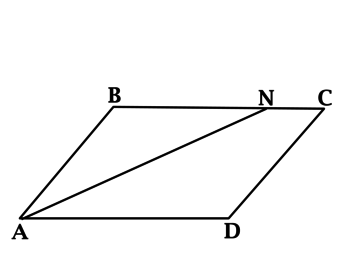
В параллелограмме \(ABCD\) проведена биссектриса \(AN\) , точка \(N\) лежит на стороне \(BC\) , причём \(NC = 3\) , \(AB = 5\) . Найдите периметр параллелограмма \(ABCD\) .
Так как внутренние накрест лежащие углы при параллельных прямых и секущей равны, то \(\angle BNA = \angle NAD\) .
Так как \(AN\) – биссектриса, то \(\angle NAD = \angle BAN\) , откуда получаем \(\angle BNA = \angle BAN\) .
Таким образом, треугольник \(ABN\) – равнобедренный, \(BN = AB\) , тогда \(BC = BN + NC = 5 + 3 = 8\) . В итоге, периметр параллелограмма \(ABCD\) равен \(8 + 8 + 5 + 5 = 26\) .
В параллелограмме \(ABCD\) на стороне \(BC\) выбрана точка \(N\) так, что \(AB = BN\) , \(\angle B = 150^<\circ>\) . Найдите \(\angle NAD\) . Ответ дайте в градусах.
Так как в равнобедренном треугольнике углы при основании равны, то \(\angle BAN = \angle BNA\) .
Так как сумма углов в треугольнике равна \(180^<\circ>\) , то \(\angle BAN = \angle BNA = 15^<\circ>\) .
Так как внутренние накрест лежащие углы при параллельных прямых и секущей равны, то \(\angle NAD = \angle BNA = 15^<\circ>\) .
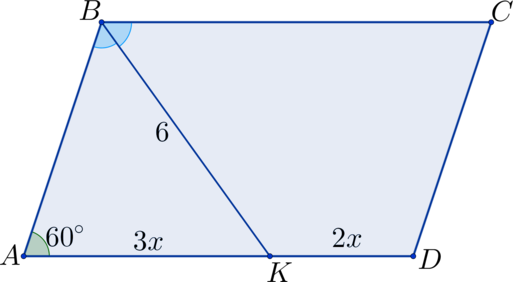
В параллелограмме \(ABCD\) биссектриса, выходящая из вершины \(B\) , пересекает \(AD\) в точке \(K\) и равна 6. \(\angle BAD = 60^\circ\) , \(AK:KD = 3:2\) . Найдите периметр параллелограмма \(ABCD\) .
\(\angle ABK = \angle KBC\) т.к. \(BK\) – биссектриса \(\angle ABC\) . \(\angle KBC = \angle BKA\) , т.к. это накрест лежащие углы при параллельных прямых. Тогда:
\[\angle ABK=\angle BKA =\frac<1><2>(180^\circ-\angle BAD)=\frac<1><2>(180^\circ-60^\circ)=60^\circ\]
\(\triangle ABK\) равносторонний, значит \(AB = BK = AK = 6\) . Тогда \(AK:KD = 6:KD = 3:2 \Rightarrow KD = 4\) . \(AD = AK + KD = 10\) , тогда:
\[P_
В параллелограмме \(ABCD\) биссектриса \(\angle BAD\) пересекает сторону \(BC\) в точке \(K\) и делит ее пополам, а также пересекает продолжение стороны \(DC\) в точке \(L\) . Найдите периметр параллелограмма, если \(CL = 3\) .
\(\triangle CKL = \triangle BKA\) и являются равнобедренными. \[AB = CL = 3, \,\,\, BC = BK + KC = 2\cdot CK = 2\cdot CL = 2\cdot 3 = 6.\] Тогда \(P_
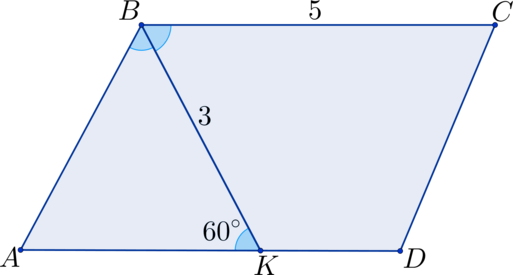
В параллелограмме \(ABCD\) : точка \(K\) лежит на стороне \(AD\) , \(BK = 3\) – биссектриса \(\angle ABC\) , \(BC = 5\) , \(\angle BKA = 60^\circ\) . Найдите периметр параллелограмма.
\(\angle ABK = \angle BKA = 60^\circ\) \(\Rightarrow\) \(\angle BAD = 60^\circ\) \(\Rightarrow\) \(\triangle ABK\) – равносторонний, тогда \(AB = BK = 3\) \(\Rightarrow\) \(P_
Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.
Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.
Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.
Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Источник