КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ — совокупность методов оценки связи между случайными явлениями и событиями, основанных на математической теории корреляции. При этом используются простейшие характеристики, требующие минимума вычислений. Термин «корреляция» обычно отождествляется с понятиями «связь» и «взаимозависимость». Однако они не адекватны. Корреляция является только одним из видов связи между признаками, к-рая проявляется в среднем и носит линейный характер. Если между двумя величинами существует однозначная связь, то такая связь называется функциональной и по одной из величин (причине) можно однозначно определить значение другой величины (следствие). Функц, зависимость является частным выражением случайной (вероятностной, стохастической) зависимости, когда связь проявляется не для каждых значений двух величин, а только в среднем.
К. а. применяется при изучении двух или большего количества случайных величин с целью выявления двух важнейших количественных характеристик: математического уравнения связи между этими величинами и оценки тесноты связи между ними. Исходными данными для определения этих характеристик служат синхронные результаты наблюдения (измерения, эксперимента), т. е. одновременно полученные из опыта статистические данные по признакам, связь между к-рыми изучается. Исходные данные могут быть заданы в виде таблиц с записями результатов наблюдения или их равноценных представлений на магнитной ленте, перфоленте или перфокартах.
К. а. нашел широкое применение в медицине и биологии для определения тесноты и уравнений связи между различными признаками, напр, результаты анализов клин, признаков или специальных обследований, проведенных над здоровыми или больными людьми (см. Корреляция функций организма). Результаты К. а. используются для составления объективных прогнозов заболеваний, оценки состояния больного, течения болезни (см. Прогнозирование). Априори, только по результатам теоретических биол, и мед. исследований, трудно или вовсе невозможно предсказать, как связаны между собой изучаемые признаки. Для того чтобы ответить на этот вопрос, проводят наблюдение или специальный эксперимент.
Двухмерный корреляционный анализ применяется при обработке опытных данных проявления каких-либо двух признаков.
Каждый результат опыта представляет собой случайную величину, а объективные закономерности проявляются только во всей совокупности результатов измерения. Поэтому выводы делаются по результатам обработки всей совокупности экспериментальных данных, а не по отдельным значениям, которые являются случайными. Для уменьшения влияния случайного события исходные данные объединяются в группы, что достигается путем составления корреляционной таблицы (см. табл.). Такая таблица содержит интервалы (или их середины) значений двух признаков — У и X, а также частоту появлений значений X и Y [mij(х, у)] в соответствующем интервале этих значений. Эти частоты, подсчитанные по результатам опыта, представляют собой практическую оценку вероятности совместного появления значений X и Y конкретного интервала. Построение корреляционной таблицы является первым этапом обработки исходной информации. Построение корреляционных таблиц и их дальнейшую полную обработку осуществляют быстро на универсальных или специализированных ЭВМ (см. Электронная вычислительная машина). По сгруппированным данным корреляционной таблицы рассчитывают эмпирические характеристики уравнения и тесноты связи. Для определения уравнения связи между Y и X рассчитывают средние значения признака Y в каждом интервале признака X. Т. о. получают для каждого i-го интервала значение Yxi, соединение которых для всех i-интервалов дает эмпирическую линию регрессии, характеризующую форму связи признака Y с признаком X в среднем — график функции Yx= f(x). Если бы между признаками Y и X существовала однозначная связь, уравнения связи было бы достаточно для решения практических и теоретических задач, т. к. с его помощью всегда можно определить значение признака Y, если задано значение X. На практике же связь между Y и X не является однозначной, эта связь является случайной и одному значению X соответствует ряд значений Y. Поэтому необходима еще одна характеристика, измеряющая силу, тесноту связи между Y и X. Такими характеристиками являются дисперсионное (корреляционное) отношение ηух и коэффициент корреляции ryx. Первая из этих величин служит характеристикой тесноты связи между Y и X в произвольной функции f, а ryx — используется только в случае, когда f является линейной функцией.
Величины ηyx и ryx также просто определяются по корреляционной таблице. Расчет обычно ведут в следующем порядке: определяют средние значения обоих признаков X и Y, их средние квадратические отклонения σx и σy, а затем ηxy по формуле:
и ryx по формуле:
где n — общее число опытов, Xcpi — среднее значение X i-го интервала, Ycpj — среднее значение Y j-го интервала, k, l — количество интервалов признаков X и Y соответственно, mi(x) — частота (количество) значений Xcpi. Количественными характеристиками точности определения ηyx и ryx служат их средние квадратические отклонения, которые равны
Значения коэффициента η лежат в пределах между нулем и единицей (0= В. Н. Райбман, Н. С. Райбман.
Источник
Основы корреляционного анализа при комплексной оценке здоровья населения
под ред. з.д.н. РФ, проф. В.С. Лучкевича
2015 Г.
УДК 614.1:614.2 (07)
Основы корреляционного анализа при комплексной оценке здоровья населения / под ред. проф. В.С. Лучкевича: учебно-методическое пособие. – СПб: Изд-во СЗГМУ им. И. И. Мечникова, 2015. – 52 с.
Авторский коллектив: В.С. Лучкевич, А. Н. Пивоваров, Г. М. Пивоварова, П.Н. Морозько, И.Л. Самодова, Е.А. Абумуслимова, Т.В. Самсонова, С.Н. Носков, Д.С. Тягунов.
Рецензент: зав. кафедрой социальной гигиены, управления и экономики здравоохранения ГБОУ ВПО СЗГМУ им. И.И. Мечникова, доктор медицинских наук, профессор Филатов Владимир Николаевич
В учебно-методическом пособии изложены основные методики использования коэффициентов корреляции в практической деятельности врача, представлены методики использования рангового метода Спирмена, коэффициента корреляции рангов Кендэла, коэффициента ассоциации и сопряженности (контингенции), коэффициента корреляции Пирсона. В учебно-методическом пособии даны методики регрессионного анализа, методики измерения связи между признаками с помощью корреляционной решетки.
Учебно-методическое пособие содержит образцы решения ситуационных задач, вопросы для самоподготовки, тестовые задания и списки литературы.
Учебно-методическое пособие предназначено для студентов лечебного, медико-профилактического и стоматологического факультетов медицинских вузов.
в качестве учебно-методического пособия методическим советом ГБОУ ВПО СЗГМУ
им. И.И.Мечникова Минздрава России
протокол № ____ от « » 2015 г.
© В.С. Лучкевич (коллектив авторов), 2015 г
ТЕМА: Основы корреляционного анализа при комплексной оценке здоровья населения.
КОНТИНГЕНТ УЧАЩИХСЯ — студенты лечебного, медико-профилактического и стоматологического факультетов медицинских вузов.
ПРОДОЛЖИТЕЛЬНОСТЬ ПРАКТИЧЕСКОГО ЗАНЯТИЯ – 4 часа (в академических часах).
Использование коэффициентов корреляции в практической деятельности врача
— ранговый метод Спирмена
— коэффициент корреляции рангов Кендэла
— коэффициенты ассоциации и сопряженности (контингенции)
— коэффициент корреляции Пирсона
— измерение связи между признаками с помощью корреляционной решетки
Решение заданий студентами самостоятельно
Решение тестовых заданий студентами
Использование коэффициентов корреляции в практической деятельности врача
Все существующие в природе связи между признаками и различными явлениями можно подразделить на функциональные и корреляционные.
Функциональные связи — это такой вид зависимости между двумя переменными величинами (количественными признаками), когда имеется строгая зависимость одной величины только от одного признака (площадь квадрата зависит от величины стороны квадрата, площадь круга – от радиуса и т.д.). Эти связи постоянны, т.е. проявляются всегда, даже в единичных наблюдениях, изучаются математическими науками и измеряются в соответствии с законами физики.
Корреляционные связи. Однако большая группа связей характеризуется такой зависимостью, когда значение одной величины изучаемых явлений (уровень смертности, средняя масса тела, длина тела и др.) определяется влиянием не одного, а многих факторов. Эти связи проявляются только при большом числе наблюдений, так как при единичных они могут не наблюдаться (при большем росте масса тела у отдельных лиц может быть меньше). Эти связи не постоянны, колеблются от нуля до единицы. Ноль означает отсутствие зависимости между признаками, а единица – полную или функциональную связь, когда имеется зависимость только от одного признака.
Указанные особенности зависимостей между признаками обусловливают необходимость различных методических подходов к их изучению. Там, где связи постоянны и проявляются всегда, они подлежат изучению точными науками, а там, где наблюдается колеблемость зависимостей между признаками, они становятся предметом изучения статистики. Поэтому корреляционные связи называются также статистическими (например, зависимость уровня заболеваемости (смертности) от возраста населения). Мерой измерения статистической зависимости служат различные коэффициенты корреляции. Оценка этих связей проводится в соответствии с данными, приведенными в табл. 1.
Источник
Методы изучения корреляционных связей
ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра гигиены, общественного здоровья и здравоохранения
( зав. кафедрой к.м.н. А.П. Дмитриев)
МЕТОДЫ ИЗУЧЕНИЯ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ
Учебно-методическое пособие для студентов
Учебно-методическое пособие “Методы изучения корреляционных связей.” подготовлено кафедрой гигиены, общественного здоровья и здравоохранения Пензенского государственного университета (заведующий кафедрой, к.м.н. Дмитриев А.П.).
В составлении принимали участие: к.м.н. Зубриянова Н.С. , Дмитриев А.П. (ответственный за подготовку Зубриянова Н.С.).
Учебно-методическое пособие подготовлено в соответствии с «Программой по общественному здоровью и здравоохранению ” для студентов лечебных факультетов высших медицинских учебных заведений”, разработанной Всероссийским учебно-научно-методическим Центром по непрерывному медицинскому и фармацевтическому образованию Минздрава России и УМЦпкп и утвержденной Руководителем департамента образовательных медицинских учреждений и кадровой политики Н.Н. Володиным в 2000 г.
Данное Учебно-методическое пособие подготовлено для студентов для самостоятельной подготовки к практическим занятиям по указанной теме.
Тема: Методы изучения корреляционных связей
— Корреляционный анализ (основные понятия)
— Коэффициент парной корреляции
— Ранговый коэффициент (Спирмена)
— Определение тесноты связи между качественными признаками (коэффициенты Шарлье, Юла, Пирсона)
Продолжительность занятия: 4 часа
Самостоятельная работа: лабораторная работа №7
В различных областях медицины, биологии, организации здравоохранения, социально-гигиенических и клинических исследованиях проводятся статистический анализ связей, изучение закономерностей и влияющих факторов.
Существуют два вида проявления количественных взаимосвязанностей между признаками (явлениями, факторами) – функциональные и корреляционные.
При функциональных зависимостях каждому значению одной переменной величины соответствует одно вполне определенное значение другой переменной. Такие зависимости наблюдаются в математике и физике. Различные измерительные приборы основаны на функциональной зависимости (высота ртутного столбика дает однозначный ответ о температуре).
Корреляционные или статистические связи, при которых численному значению одной переменной соответствует много значений другой переменной. Пример, между ростом и весом детей существует бесспорная зависимость, но это не значит, что определенному росту строго соответствует определенный вес. В силу участия в формировании веса многих других факторов, каждому значению роста соответствует несколько значений веса, которые могут быть выражены в виде распределения.
Функциональная связь имеет место по отношению к каждому конкретному наблюдению. Корреляционная проявляется в среднем для всей совокупности наблюдений. выявления взаимодействия факторов, определение силы и направленности Практическое использование корреляционного анализа: выявление взаимодействия факторов, определение силы и направления влияния одних факторов на другие.
Следует подчеркнуть, что определение наличия связи между явлениями и факторами – дело специалистов. Статистика лишь измеряет эту связь.
Корреляционная зависимость отличается по форме связи, ее направлению и силе. Ориентировочное представление о характере зависимости между двумя изученными факторами дает графический анализ (так называемая «скэттер-диаграмма»), который позволяет рассмотреть концентрацию и рассеивание точек на пересечении координат изучаемых признаков в определенном направлении вокруг линии регрессии.
Форма связи может быть прямолинейной и криволинейной. Прямолинейная связь – равномерные изменения одного признака соответствуют равномерным изменениям второго признака при незначительных отклонениях. Криволинейная связь – равномерные изменения одного признака соответствуют неравномерным изменениям второго признака.
Направление связи может быть прямое (положительное) или обратное (отрицательное). Если с увеличением одного признака второй также увеличивается или с уменьшением одного другой тоже уменьшается, зависимость прямая, положительная. Если с увеличением одного признака другой уменьшается или с уменьшением первого признака второй увеличивается, зависимость обратная, отрицательная.
По силе связи зависимость может быть сильная (сильно выражена), средняя (умеренно выражена), слабая (слабо выражена).
Оценка силы связи по величине коэффициента корреляции
| Размер связи | Характер связи | |
| Прямая (+) | Обратная (-) | |
| Отсутствует | ||
| Слабая | От 0 до +0,29 | От 0 до -0,29 |
| Средняя | От +0,3 до +0,69 | От -0,3 до -0,69 |
| Сильная | От +0,7 до +0,99 | От -0,7 до -0,99 |
| Полная (функциональная) | +1,0 | -1,0 |
Количественная характеристика взаимосвязи изучаемых признаков может быть дана на основании вычисления показателей силы связи между ними (коэффициенты корреляции) и определения зависимости одного признака от изменения другого (коэффициент регрессии).
Коэффициент парной корреляции
Коэффициент парной корреляции вычисляется по формуле:
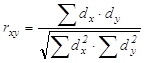
Алгоритм расчета коэффициента парной корреляции:
1) записывают исходные данные в два вариационных ряда – x и y;
2) вычисляют среднюю арифметическую ряда x и y;
3) определяют разность между членом ряда и средними величинами;
4) перемножают разности ряда x и y между собой;
5) находят сумму перемножаемых разностей (с учетом арифметического знака);
6) возводят в квадрат каждую разность (отклонение) ряда х и у;
7) определяют сумму квадратов отклонений (разностей) для ряда х и у отдельно;
8) подставляют полученные данные в исходную формулу и вычисляют коэффициент парной корреляции.
Пример. Определить корреляционную связь между строками введения противодифтерийной сыворотки и летальностью от этого заболевания.
Источник